​量化指标之阿尔法、贝塔

量化指标之阿尔法、贝塔

什么是贝塔β？

β系数是一种风险指标，用来衡量单只基金或股票相对于整个市场的价格波动情况。β的绝对值越大（上限是1），表示其收益变化与市场的变化关联越紧密。

举个例子，单只基金或股票的β值是0.8（不考虑其他情况），那么如果大盘上涨10%，这只基金或股票会上涨0.8*10%=8%。如果大盘下跌10%，它也随之下跌8%。

β系数取值范围是-1到1，如果为负是什么意思呢？这种情况下，表示这只基金或股票与市场行情相反，大盘上涨，它下跌，反之亦然。

什么是阿尔法α？

要弄明白α，需要先简单了解一下资本资产定价模型，这个模型比较简单：

期望收益率＝无风险回报率＋β*（整体股市回报率－无风险回报率）

其中，无风险回报率一般取央行公布的一年期定期存款利率（默认存在银行是无风险的）。

根据这个模型，在知道单只基金或股票的β系数、整体股市回报率、无风险利率的情况下，那么它的预期收益率也就可以计算出来了。

比如，如果市场期望收益率为10%，某只基金的β值为1.1，无风险收益率为6%，那么根据上面资本资产定价模型，这只基金的预期收益率=6% + 1.1*（10%-6%）=10.4%。

但是我们知道，如果现实的资本市场能够由一个公式定义，那也就没有套利空间，股价也不可能随时变动了。如果这只基金真实的收益率是15%，那上面计算出来的预期收益率10.4%该如何自处呢？预测不准，经济学家好尴尬，于是就发明了一个阿尔法α，来表示两者的差值，阿尔法α = 15% - 10.4% = 4.6%。

仔细想想，这个阿尔法α指标也有现实的意义。α越大，是不是表示这只基金超过大家对它期望（根据β、大盘整体回报率等计算得到的）的收益越多呢？毫无疑问，如果一只基金的α越大，它的基金经理肯定会受到追捧。

如何计算？

β = 单只股票或基金与整体市场的协方差 / 市场的方差

α = 单只股票或基金实际收益率 - 无风险回报 - β*（整体股市回报率－无风险回报率）

Python实践环节

1、读取数据

import pandas as pd import numpy as np import matplotlib.pyplot as plt # 读取单只基金数据 df_fund = pd.read_csv('data/150018.SZ.csv') df_fund.head()

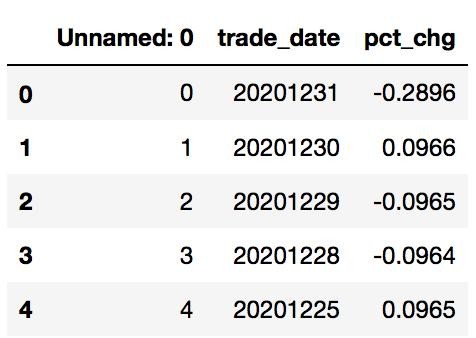
# 读取深证的指数数据 df_index = pd.read_csv('data/399300.SZ.csv') df_index.head()

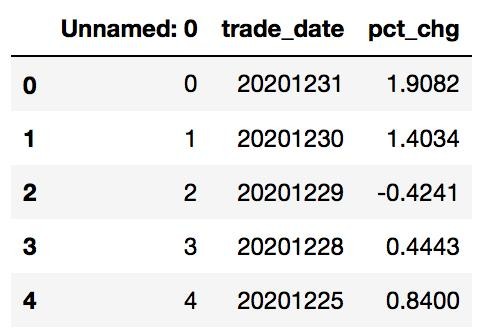
2、计算Beta

# 150018基金与深证市场的协方差 cov = df_fund['pct_chg'].cov(df_index['pct_chg']) # 深证市场的方差 sigma = df_index['pct_chg'].cov(df_index['pct_chg']) # 计算Beta beta = cov / sigma beta0.014058426975435948

3、计算alpha

# prod函数是将某一列数据连乘 # 计算深证的整体收益率 df_index.loc[:,'pct_chg'] /= 100 df_index.loc[:, 'pct_chg'] += 1 market_yeild = df_index['pct_chg'].prod(axis=0) - 1 market_yeild10.496181477259768# 计算单只基金的收益率 df_fund.loc[:, 'pct_chg'] /= 100 df_fund.loc[:, 'pct_chg'] += 1 single_fund_yeild = df_fund['pct_chg'].prod(axis=0) - 1 single_fund_yeild10.267164717193765# 无风险利率，取一年期定期存款利率 rf = 0.015 # 计算alpha alpha = single_fund_yeild - (rf + beta * (market_yeild - rf)) alpha10.104815792779418